2026
-
-
Never Saddle for Reparameterized Steepest Descent as Mirror Flow
Tom Jacobs, Chao Zhou, and Rebekka Burkholz
ICLR (2026)
ABSTRACT BIB
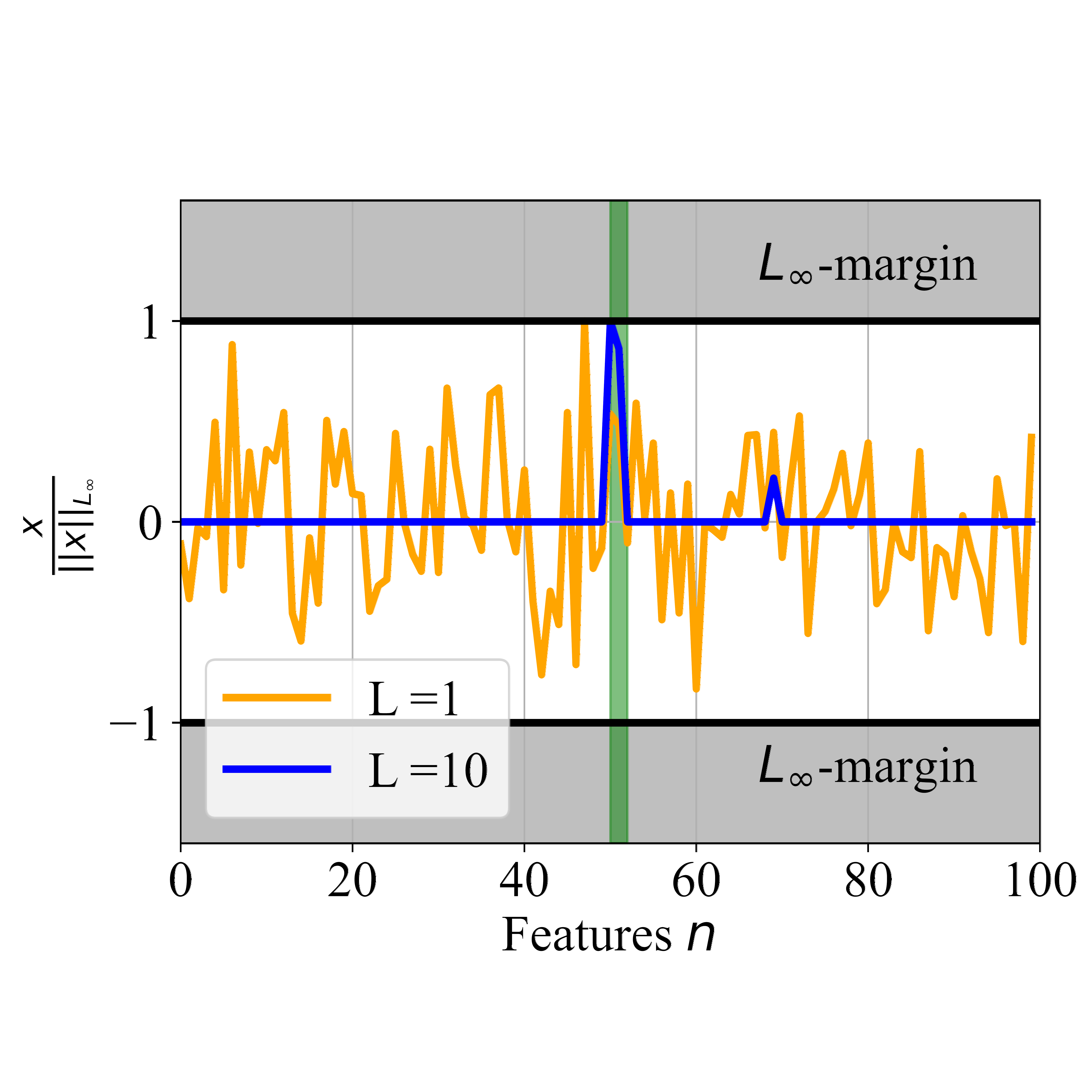
What distinguishes modern adaptive methods from gradient descent to favor better generalizing solutions? To study this question for steepest-descent methods, including sign descent (an optimizer closely related to Adam), we introduce steepest mirror flows as a unifying theoretical framework. This enables us to analyze how optimization geometry governs learning dynamics, implicit bias, and sparsity. It also suggests a mechanism that may help explain why Adam and AdamW often outperform SGD in fine-tuning. Focusing on diagonal linear networks and deep diagonal linear reparameterizations, we show that steeper descent promotes saddle-point escape. By contrast, gradient descent typically requires much larger learning rates to escape saddles—regimes that are less common in fine-tuning practice. Furthermore, we find that decoupled weight decay, as in AdamW, stabilizes sparse training by enforcing novel balance equations. Empirical experiments establish that our theoretical insights and hypothesized mechanisms transfer to realistic settings. Together, these results identify two mechanisms through which steepest descent can benefit modern optimization: saddle escape and sparsity.@inproceedings{ Jacobs2026never, title={Never Saddle for Reparameterized Steepest Descent as Mirror Flow}, author={Tom Jacobs and Chao Zhou and Rebekka Burkholz}, booktitle={The Fourteenth International Conference on Learning Representations}, year={2026}, url={https://openreview.net/forum?id=YgudIlQ9nC} }
-
-
Hyperbolic Aware Minimization: Implicit Bias for Sparsity
Tom Jacobs, Advait Gadhikar, Celia Rubio-Madrigal, and Rebekka Burkholz
ICLR (2026)
ABSTRACT BIB
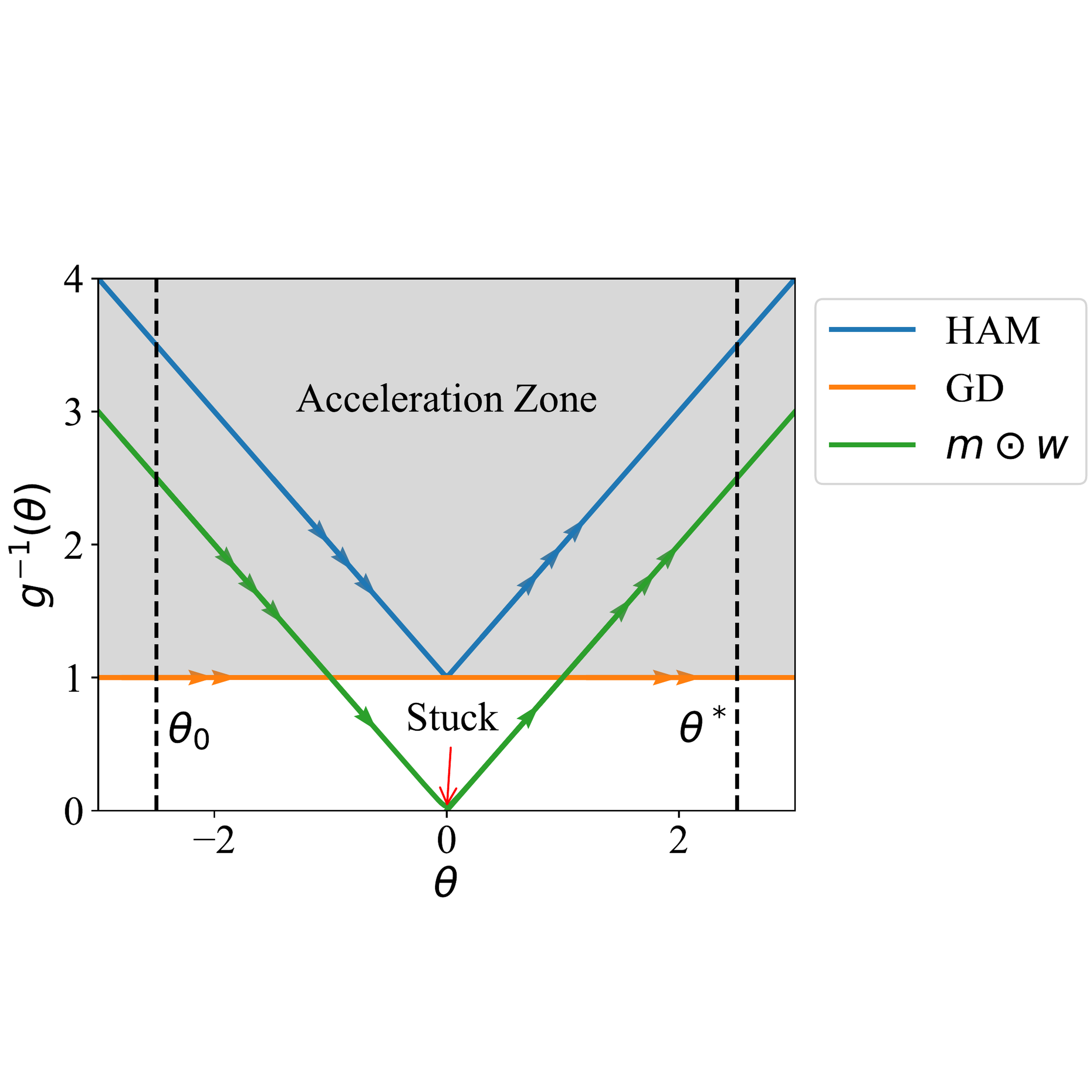
Understanding the implicit bias of optimization algorithms is key to explaining and improving the generalization of deep models. The hyperbolic implicit bias induced by pointwise overparameterization promotes sparsity, but also yields a small inverse Riemannian metric near zero, slowing down parameter movement and impeding meaningful parameter sign flips. To overcome this obstacle, we propose Hyperbolic Aware Minimization (HAM), which alternates a standard optimizer step with a lightweight hyperbolic mirror step. The mirror step incurs less compute and memory than pointwise overparameterization, reproduces its beneficial hyperbolic geometry for feature learning, and mitigates the small–inverse-metric bottleneck. Our characterization of the implicit bias in the context of underdetermined linear regression provides insights into the mechanism how HAM consistently increases performance extemdash even in the case of dense training, as we demonstrate in experiments with standard vision benchmarks. HAM is especially effective in combination with different sparsification methods, advancing the state of the art.@inproceedings{ jacobs2025ham, title={Hyperbolic Aware Minimization: Implicit Bias for Sparsity}, author={Tom Jacobs and Advait Gadhikar and Celia Rubio-Madrigal and Rebekka Burkholz}, booktitle={The Fourteenth International Conference on Learning Representations}, year={2026}, url={https://openreview.net/forum?id=XKB5Hu0ACY} }
2025
-
-
The Graphon Limit Hypothesis: Understanding Neural Network Pruning via Infinite Width Analysis
Hoang Pham, The-Anh Ta, Tom Jacobs, Rebekka Burkholz and Long Tran-Thanh
NeurIPS (2025)
ABSTRACT BIB
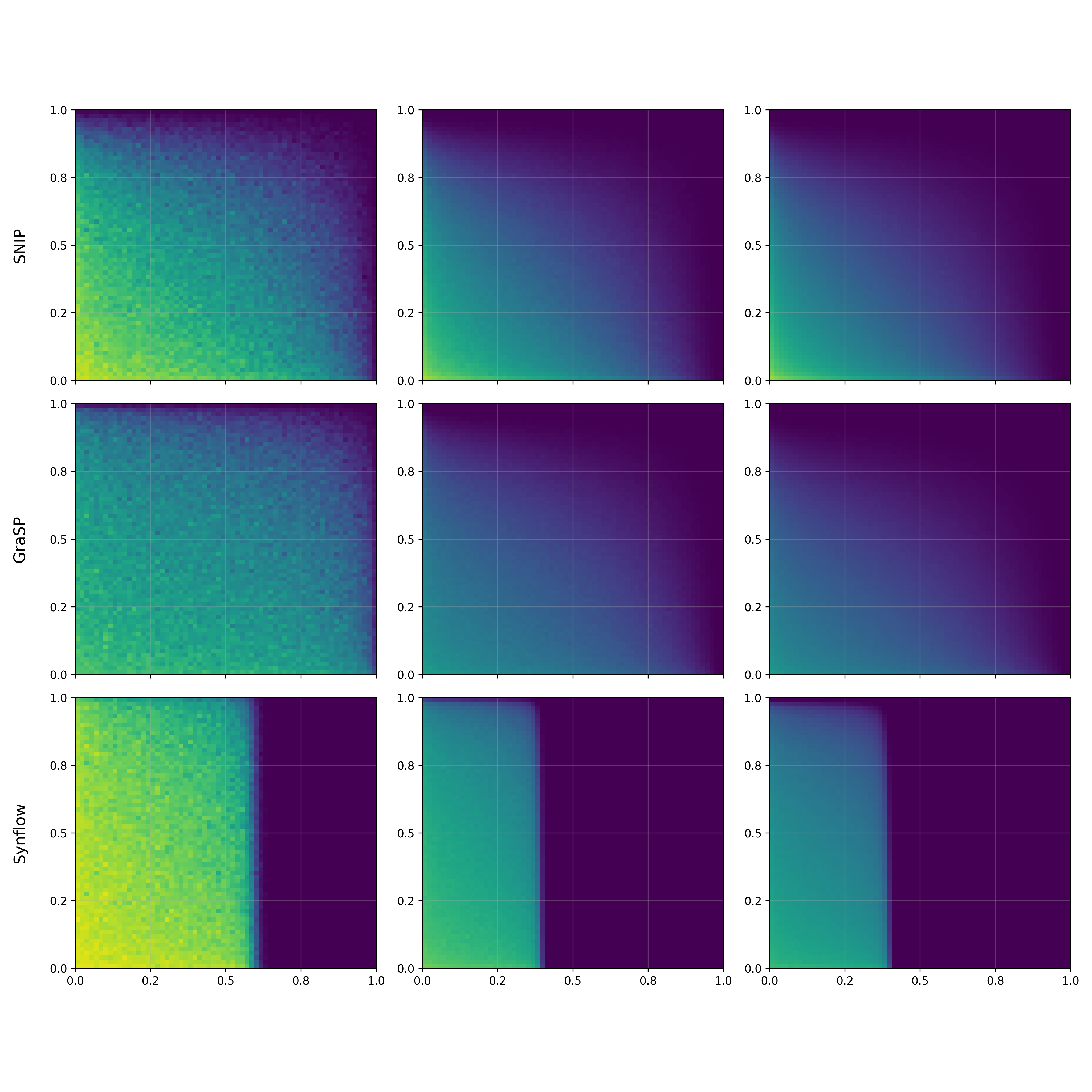
Sparse neural networks promise efficiency, yet training them effectively remains a fundamental challenge. Despite advances in pruning methods that create sparse architectures, understanding why some sparse structures are better trainable than others with the same level of sparsity remains poorly understood. Aiming to develop a systematic approach to this fundamental problem, we propose a novel theoretical framework based on the theory of graph limits, particularly graphons, that characterizes sparse neural networks in the infinite-width regime. Our key insight is that connectivity patterns of sparse neural networks induced by pruning methods converge to specific graphons as networks' width tends to infinity, which encodes implicit structural biases of different pruning methods. We postulate the Graphon Limit Hypothesis and provide empirical evidence to support it. Leveraging this graphon representation, we derive a Graphon Neural Tangent Kernel (Graphon NTK) to study the training dynamics of sparse networks in the infinite width limit. Graphon NTK provides a general framework for the theoretical analysis of sparse networks. We empirically show that the spectral analysis of Graphon NTK correlates with observed training dynamics of sparse networks, explaining the varying convergence behaviours of different pruning methods. Our framework provides theoretical insights into the impact of connectivity patterns on the trainability of various sparse network architectures.@inproceedings{ anonymous2025the, title={The Graphon Limit Hypothesis: Understanding Neural Network Pruning via Infinite Width Analysis}, author={Anonymous}, booktitle={The Thirty-ninth Annual Conference on Neural Information Processing Systems}, year={2025}, url={https://openreview.net/forum?id=EEZLBhyer1} }
-
-
Pay Attention to Small Weights
Chao Zhou, Tom Jacobs, Advait Gadhikar, and Rebekka Burkholz
NeurIPS (2025)
ABSTRACT BIB
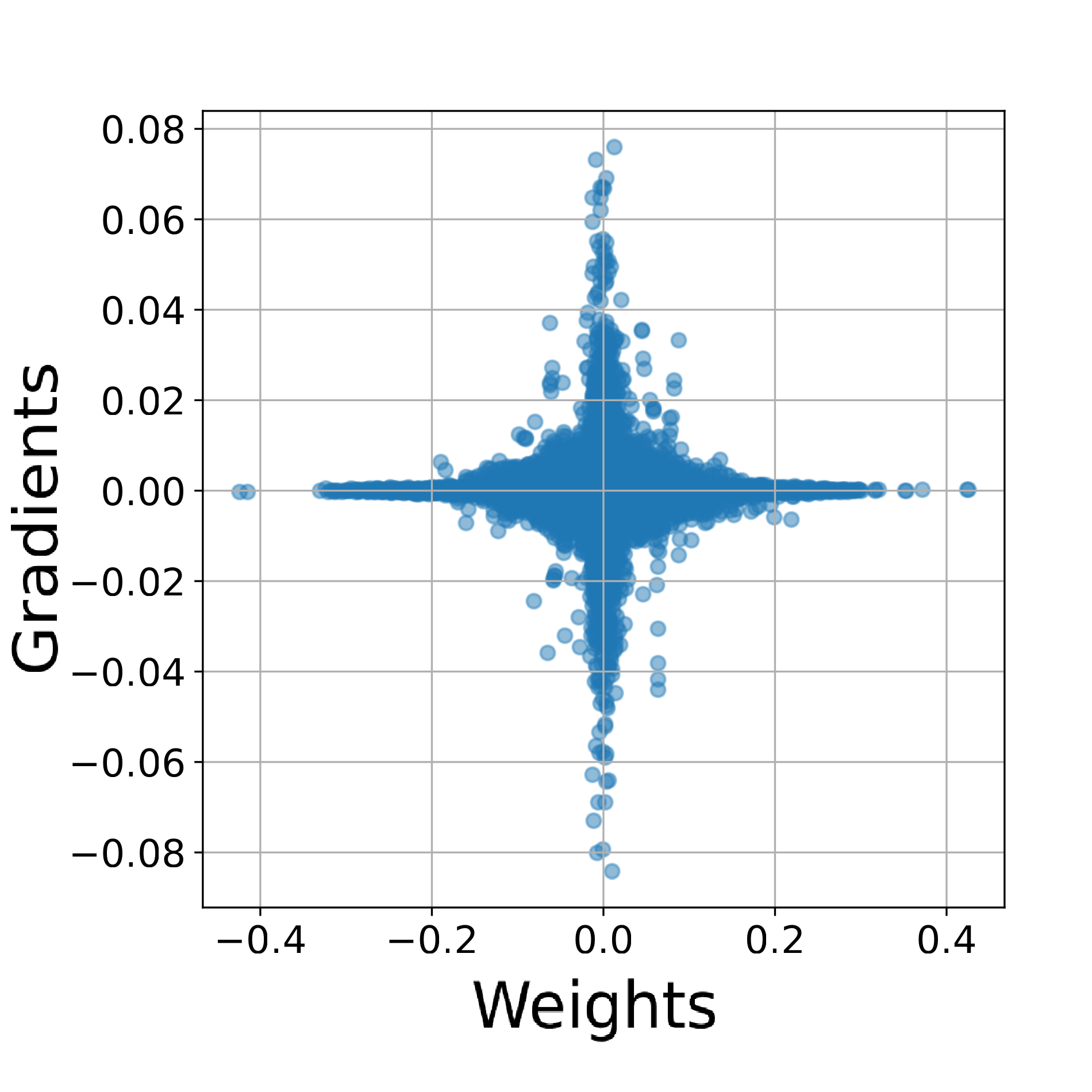
Finetuning large pretrained neural networks is known to be resource-intensive, both in terms of memory and computational cost. To mitigate this, a common approach is to restrict training to a subset of the model parameters. By analyzing the relationship between gradients and weights during finetuning, we observe a notable pattern: large gradients are often associated with small-magnitude weights. This correlation is more pronounced in finetuning settings than in training from scratch. Motivated by this observation, we propose NANOADAM, which dynamically updates only the small-magnitude weights during finetuning and offers several practical advantages: first, this criterion is gradient-free -- the parameter subset can be determined without gradient computation; second, it preserves large-magnitude weights, which are likely to encode critical features learned during pretraining, thereby reducing the risk of catastrophic forgetting; thirdly, it permits the use of larger learning rates and consistently leads to better generalization performance in experiments. We demonstrate this for both NLP and vision tasks.@inproceedings{ zhou2025payattentionsmallweights, title={Pay Attention to Small Weights}, author={Chao Zhou and Tom Jacobs and Advait Gadhikar and Rebekka Burkholz}, booktitle={The Thirty-ninth Annual Conference on Neural Information Processing Systems}, year={2025}, url={https://openreview.net/forum?id=XKnOA7MhCz} }
-
-
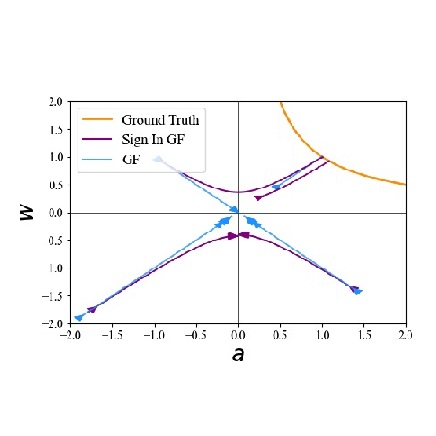
Sign-In to the Lottery: Reparameterizing Sparse Training
Advait Gadhikar*, Tom Jacobs*, Chao Zhou, and Rebekka Burkholz
NeurIPS (2025)
ABSTRACT BIB
The performance gap between training sparse neural networks from scratch (PaI) and dense-to-sparse training presents a major roadblock for efficient deep learning. According to the Lottery Ticket Hypothesis, PaI hinges on finding a problem specific parameter initialization. As we show, to this end, determining correct parameter signs is sufficient. Yet, they remain elusive to PaI. To address this issue, we propose Sign-In, which employs a dynamic reparameterization that provably induces sign flips. Such sign flips are complementary to the ones that dense-to-sparse training can accomplish, rendering Sign-In as an orthogonal method. While our experiments and theory suggest performance improvements of PaI, they also carve out the main open challenge to close the gap between PaI and dense-to-sparse training.@inproceedings{ Gadhikar2025SignInTT, title={Sign-In to the Lottery: Reparameterizing Sparse Training}, author={Advait Gadhikar and Tom Jacobs and Chao Zhou and Rebekka Burkholz}, booktitle={The Thirty-ninth Annual Conference on Neural Information Processing Systems}, year={2025}, url={https://openreview.net/forum?id=iwKT7MEZZw} }
-
-
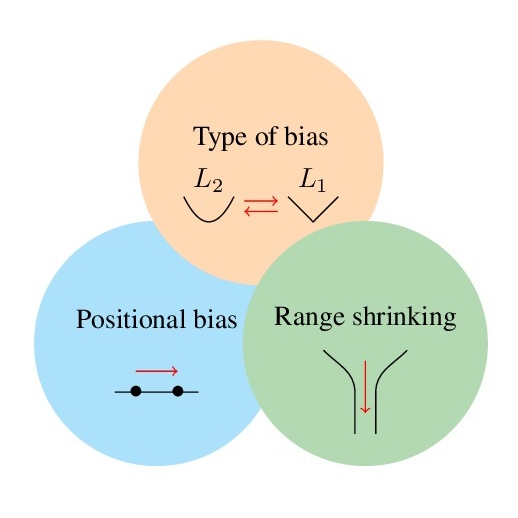
Mirror, Mirror of the Flow: How Does Regularization Shape Implicit Bias?
Tom Jacobs, Chao Zhou, and Rebekka Burkholz
ICML (2025)
ABSTRACT BIB
Implicit bias plays an important role in explaining how overparameterized models generalize well. Explicit regularization like weight decay is often employed in addition to prevent overfitting. While both concepts have been studied separately, in practice, they often act in tandem. Understanding their interplay is key to controlling the shape and strength of implicit bias, as it can be modified by explicit regularization. To this end, we incorporate explicit regularization into the mirror flow framework and analyze its lasting effects on the geometry of the training dynamics, covering three distinct effects: positional bias, type of bias, and range shrinking. Our analytical approach encompasses a broad class of problems, including sparse coding, matrix sensing, single-layer attention, and LoRA, for which we demonstrate the utility of our insights. To exploit the lasting effect of regularization and highlight the potential benefit of dynamic weight decay schedules, we propose to switch off weight decay during training, which can improve generalization, as we demonstrate in experiments.@inproceedings{ jacobs2025mirror, title={Mirror, Mirror of the Flow: How Does Regularization Shape Implicit Bias?}, author={Tom Jacobs and Chao Zhou and Rebekka Burkholz}, booktitle={Forty-second International Conference on Machine Learning}, year={2025}, url={https://api.semanticscholar.org/CorpusID:277857621} }
-
-
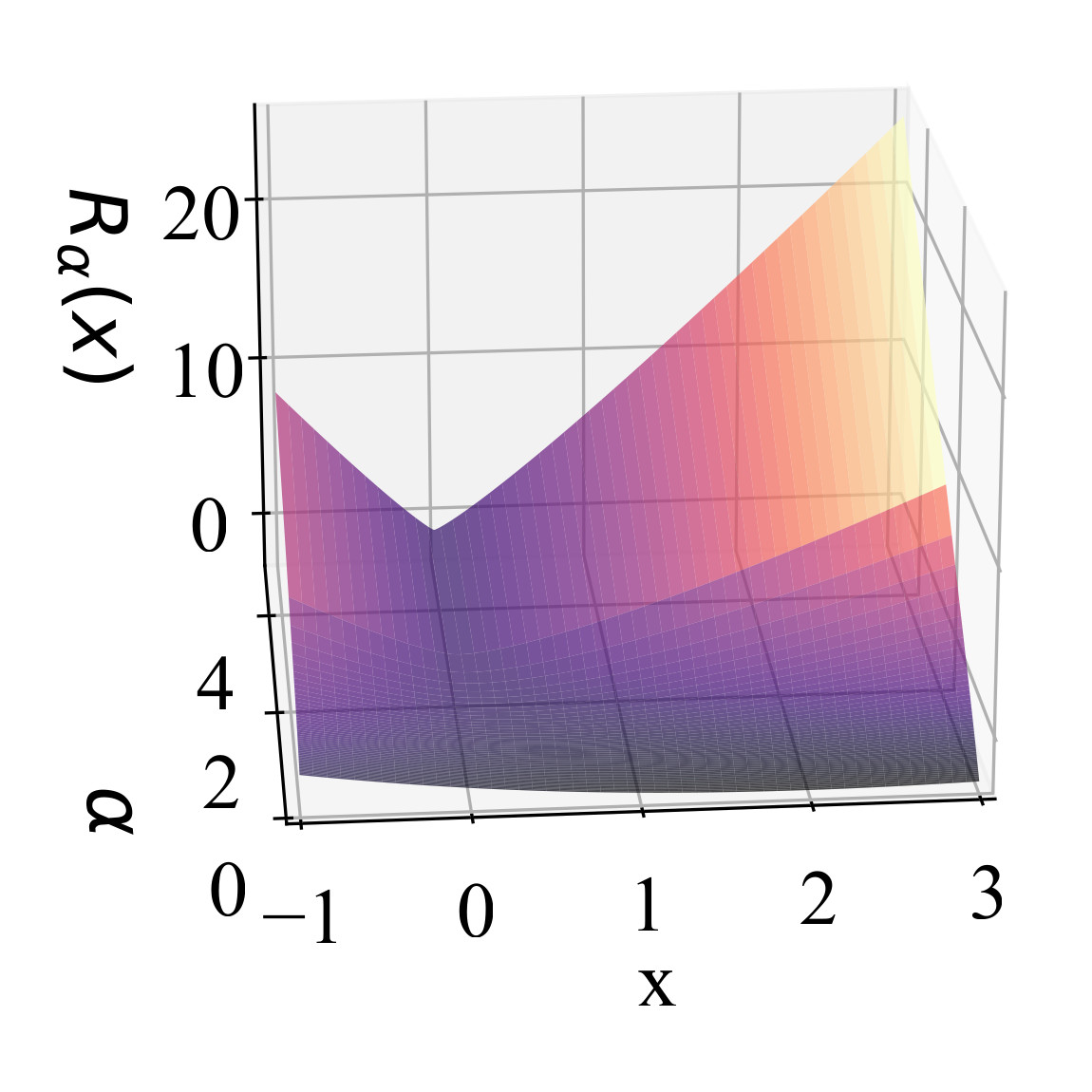
Mask in the Mirror: Implicit Sparsification
Tom Jacobs and Rebekka Burkholz
ICLR (2025)
ABSTRACT BIB
Continuous sparsification strategies are among the most effective methods for reducing the inference costs and memory demands of large-scale neural networks. A key factor in their success is the implicit L1 regularization induced by jointly learning both mask and weight variables, which has been shown experimentally to outperform explicit L1 regularization. We provide a theoretical explanation for this observation by analyzing the learning dynamics, revealing that early continuous sparsification is governed by an implicit L2 regularization that gradually transitions to an L1 penalty over time. Leveraging this insight, we propose a method to dynamically control the strength of this implicit bias. Through an extension of the mirror flow framework, we establish convergence and optimality guarantees in the context of underdetermined linear regression. Our theoretical findings may be of independent interest, as we demonstrate how to enter the rich regime and show that the implicit bias can be controlled via a time-dependent Bregman potential. To validate these insights, we introduce PILoT, a continuous sparsification approach with novel initialization and dynamic regularization, which consistently outperforms baselines in standard experiments.@inproceedings{ jacobs2025mask, title={Mask in the Mirror: Implicit Sparsification}, author={Tom Jacobs and Rebekka Burkholz}, booktitle={The Thirteenth International Conference on Learning Representations}, year={2025}, url={https://openreview.net/forum?id=U47ymTS3ut} }